Osservare i 12 resistori disposti come nello schizzo. Tutti i resistori hanno uguale resistenza pari a R.
Quanto vale la resistenza equivalente misurata tra A e B ?
Non basta la risposta (per la quale basterebbe un qualsiasi simulatore circuitale), bisogna anche spiegarla
Per la serie: non esiste solo il DX

Quanto vale la resistenza equivalente misurata tra A e B ?
Non basta la risposta (per la quale basterebbe un qualsiasi simulatore circuitale), bisogna anche spiegarla

Per la serie: non esiste solo il DX

 . Se poi uno dei suddetti puntali è posizionato sul centrale di un SO 239 e si è in zona 5, si riesce anche a lavorare K9W in 10 metri
. Se poi uno dei suddetti puntali è posizionato sul centrale di un SO 239 e si è in zona 5, si riesce anche a lavorare K9W in 10 metri 
 ). Sono indicate le correnti nei rami e il potenziale nei nodi (alimentazione 12 V, resistenze da 1000 Ohm):
). Sono indicate le correnti nei rami e il potenziale nei nodi (alimentazione 12 V, resistenze da 1000 Ohm):

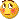


Commenta